一、矩形面积
难度:中等
题目传送门:矩形面积
题目
给你二维平面上两个由直线构成且边与坐标轴平行/垂直的矩形,请你计算并返回两个矩形覆盖的总面积。
每个矩形由其 左下 顶点和 右上 顶点坐标表示:
- 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
- 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。
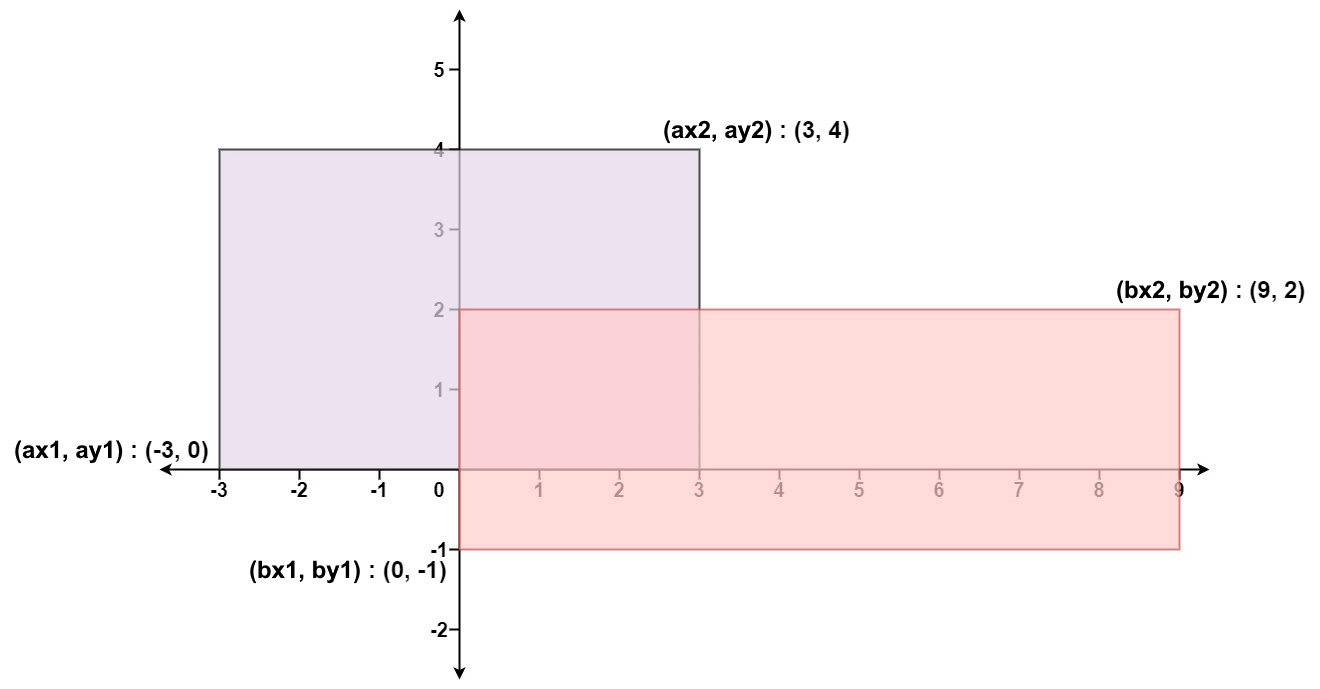
示例 1:
输入:ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出:45
示例 2:
输入:ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出:16
提示:
- -10^4 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 10^4
思路
求覆盖面积,那么重点是重叠的面积只能算一次,即总面积=两个矩形面积 - 重叠面积。
另通过左下顶点和右上顶点可以得出几个隐含条件:
- ax2 > ax1
- bx2 > bx1
- bx2 > bx1
- by2 > by1
反映到坐标轴上,就是计算重叠的w和h。
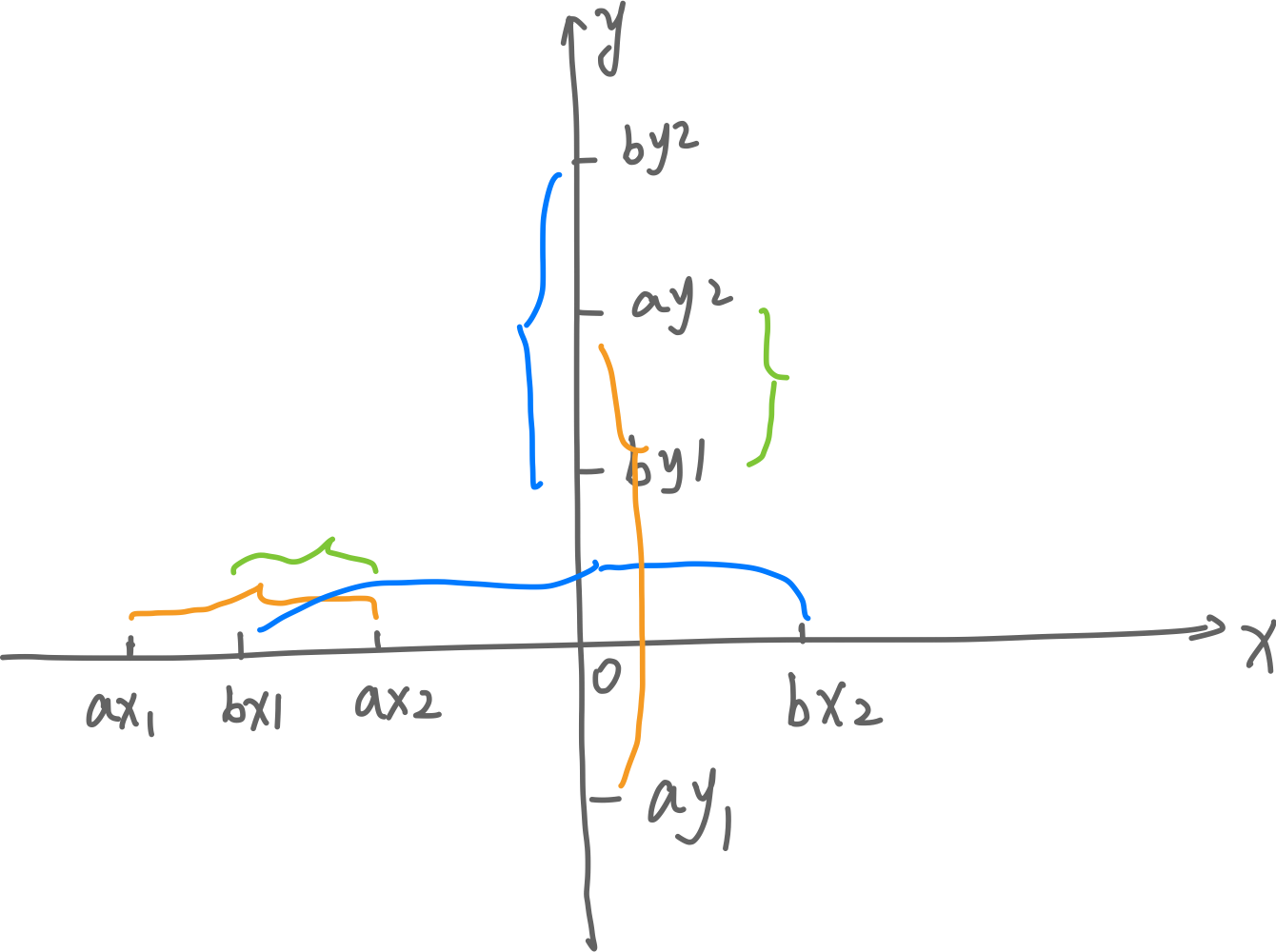
绿色部分为重叠部分,可以看出:
- w = min(ax2,bx2) - max(ax1,bx1)
- h = min(ay2,by2) - max(ay1,by1)
如果w或者h为负数或者0,则表示重叠为0,最终结果就是减去重叠面积即可。
这种方法下:
- 时间复杂度为O(1);
- 空间复杂度为O(1)。
代码
先上测试
func Test_computeArea(t *testing.T) {
inputs := [][]int{ \{-3, 0, 3, 4, 0, -1, 9, 2 \}, \{-2, -2, 2, 2, -2, -2, 2, 2\}, \{-2, -2, 2, 2, 3, 3, 4, 4\}}
expects := []int{45, 16, 17}
for i := 0; i < len(inputs); i++ {
got := computeArea(inputs[i][0], inputs[i][1], inputs[i][2], inputs[i][3], inputs[i][4], inputs[i][5], inputs[i][6], inputs[i][7])
expected := expects[i]
if got != expected {
t.Fatalf("[%d,%v] want %d,got %d", i+1, inputs[i], expected, got)
}
}
}
方法实现:
func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
area := (ax2-ax1)*(ay2-ay1) + (bx2-bx1)*(by2-by1)
w := min(ax2, bx2) - max(ax1, bx1)
if w <= 0 {
return area
}
h := min(ay2, by2) - max(ay1, by1)
if h <= 0 {
return area
}
return area - w*h
}
func min(x, y int) int {
if x < y {
return x
}
return y
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
性能
来自Leetcode, 0表示小于1个单位。
- 执行用时: 20 ms
- 内存消耗: 6 MB
二、移掉K位数字
难度:中等
题目传送门:移掉K位数字
题目
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
示例 1 :
输入:num = "1432219", k = 3
输出:"1219"
解释:移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。
示例 2 :
输入:num = "10200", k = 1
输出:"200"
解释:移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入:num = "10", k = 2
输出:"0"
解释:从原数字移除所有的数字,剩余为空就是 0 。
提示:
- 1 <= k <= num.length <= 10^5
- num 仅由若干位数字(0 - 9)组成
- 除了 0 本身之外,num 不含任何前导零
思路
要最终的数字最小,高位的k个数一定是保持递增的,否则就不是最小的。
按照这个思路,在删除k个数之前,从左往右判断,如果上一个数比下一个大,则删除上一个。
如果结果没有删除到k个数,即遍历完成,此时结果数列是递增的。那么就需要剪尾,把排列在最后的数进行删除。
需要注意提示3,结果数不能包含前导零,所以结果遍历去掉0。
这种方法下:
- 每个元素都要进入结果数,时间复杂度为O(n);
- 需要一个数组来保存结果,空间复杂度为O(n)。
代码
先上测试
func Test_computeArea(t *testing.T) {
type Item struct {
num string
k int
}
inputs := []Item{\{num: "1432219", k: 3\}, \{"10200", 1\}, \{"10", 2\}, \{"9", 1\}, \{"10200", 1\}, \{"10", 1\}, \{"100", 1\}}
expects := []string{"1219", "200", "0", "0", "200", "0", "0"}
for i := 0; i < len(inputs); i++ {
got := removeKdigits(inputs[i].num, inputs[i].k)
expected := expects[i]
if got != expected {
t.Fatalf("[%d,%v] want %v,got %v", i+1, inputs[i], expected, got)
}
}
}
方法实现:
func removeKdigits(num string, k int) string {
if k <= 0 {
return num
}
var result []byte
index := -1
m := 0
for i := 0; i < len(num); i++ {
if index == -1 {
result = append(result, num[i])
index++
continue
}
if m == k {
result = append(result, num[i:]...)
break
}
for index > -1 && m < k && num[i] < result[index] {
result = result[:len(result)-1]
index--
m++
}
result = append(result, num[i])
index++
}
if m < k {
// 剪尾
if len(result) <= k-m {
return "0"
} else {
result = result[:len(result)-k+m]
}
}
// 去除头部0
r := strings.TrimLeft(string(result), "0")
if r == "" {
r = "0"
}
return r
}
性能
来自Leetcode, 0表示小于1个单位。
- 执行用时: 4 ms
- 内存消耗: 4.3 MB
tips: 不得不吐槽,同样的代码在leetcode运行结果不一致。