验证二叉搜索树

一、接雨水

难度：中等

题目传送门：验证二叉搜索树

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

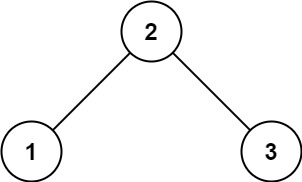
输入：root = [2,1,3]

输出：true

示例 2：

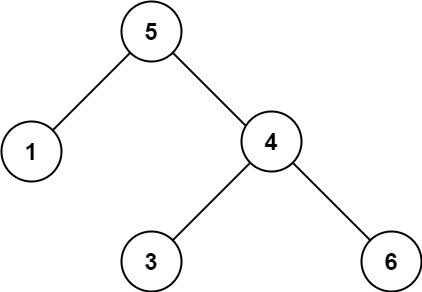
输入：root = [5,1,4,null,null,3,6]

输出：false

解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-2^31 <= Node.val <= 2^31 - 1

思路

要确保是正确的二叉搜索树，则需要保证左小右大。如果所有父节点均满足此要求，则二叉搜索树合法。

由此可以看出这是一道典型的递归题。从root节点开始，如果左子树存在，则左子树成为判断的子树；同理右子树也是一样。

由于是二叉搜索树，则按照中序遍历的方法，则打印出来的结果应该是递增的序列。反映到算法上，则上一个节点值需要小于下一个节点值。

实现起来，先判断左节点，然后判断parent，然后判断右节点。保留上一个节点的值，当判断当前节点（current parent node）的时候，比较其大小，如果上一个节点值大于或者等于当前节点值，则返回false。

这种方法下：

每一个元素需要一次遍历，时间复杂度为O(n)；
需要保留上一个节点值,空间复杂度为O(1)。（实现时要考虑到递归产生的方法栈，实际消耗的内存会比较多）

代码

先上测试

func Test_numTrees(t *testing.T) {
	d1 := &TreeNode{
		Val:   2,
		Left:  &TreeNode{Val: 1},
		Right: &TreeNode{Val: 3},
	}
	d2 := &TreeNode{
		Val:  5,
		Left: &TreeNode{Val: 1},
		Right: &TreeNode{Val: 4,
			Left:  &TreeNode{Val: 3},
			Right: &TreeNode{Val: 6},
		},
	}
	d3 := &TreeNode{
		Val: 0,
	}
	d4 := &TreeNode{
		Val:  1,
		Left: &TreeNode{Val: 1},
	}
	// 根据题意，对边界做一个测试
	d5 := &TreeNode{
		Val: -2147483648,
	}

	inputs := []*TreeNode{d1, d2, d3, d4, d5}
	expects := []bool{true, false, true, false, true}
	for i := 0; i < len(inputs); i++ {
		got := isValidBST(inputs[i])
		expected := expects[i]
		if expected != got {
			t.Errorf("[%d] want %v,got %v", i+1, expected, got)
		}
	}
}

方法实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

var pre int

func isValidBST(root *TreeNode) bool {
	// 每次进来重置pre
	pre = 1 << 31 * -1 -1
	return helper(root)
}

func helper(root *TreeNode) bool {
	if root == nil {
		return true
	}
	if !helper(root.Left) {
		return false
	}
	if root.Val <= pre {
		return false
	}
	pre = root.Val
	return helper(root.Right)
}

性能

来自Leetcode, 0表示小于1个单位。

执行用时: 8 ms

内存消耗: 5 MB