不同的二叉搜索树

一、不同的二叉搜索树

难度：中等

题目

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种？返回满足题意的二叉搜索树的种数。

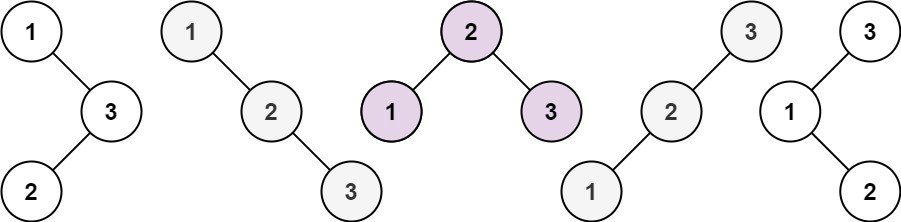
示例 1：
    输入：n = 3
    输出：5
示例 2：
    输入：n = 1
    输出：1

提示：

1 <= n <= 19

思路

题干可以提取几个要求：

只有n个节点，且节点值唯一；
每个二叉树是二叉排序数，即左小右大；
每个二叉排序树要用全部的节点点n个。

n个节点，则存在n种root节点的二叉排序树，所以总数 = n * 以i为root节点的二叉树的数量, 转换为几何表达式： G(n) = f(1) + f(2) + ... + f(i) + ... + f(n)

对于f(i),root节点i的左子树有节点(i-1)个，右子树有节点（n-i）个，左右子树又是需要计算可能存在的包含多个节点的二叉树，则： f(i) = G(i-1) * G(n-i)

综合两式，得：G(n) = G(0) * G(n-1) + G(1)*G(n-2) + ... + G(i-1) * G(n-i) + ... + G(n-1) * G(0)

代码

先写测试

func Test_numTrees(t *testing.T) {
	inputs := []int{1, 3}
	expects := []int{1, 5}
	for i := 0; i < len(inputs); i++ {
		got := numTrees(inputs[i])
		expected := expects[i]
		if expected != got {
			t.Errorf("[%d] want %d,got %d", i+1, expected, got)
		}
	}
}

方法实现

func numTrees(n int) int {
	G := make([]int, n+1)
	// 如果只有1个节点或者0个节点需要构建子二叉树，则可能只有一种
	G[0], G[1] = 1, 1
	// G(n) = G(0) * G(n-1) + G(1)*G(n-2) + ... + G(i-1) * G(n-i) + ... + G(n-1) * G(0)
	for root := 2; root <= n; root++ {
		for parent := 1; parent <= root; parent++ {
			G[root] += G[parent-1] * G[root-parent]
		}
	}
	return G[n]
}

性能

来自Leetcode, 0表示小于1个单位。

执行用时: 0ms

内存消耗: 1.8 MB